Les Turbulences
A propos des argiles Vie Espace Temps®
Dans les années trente, A.N. Kolmogorov a proposé une description mathématique donnant une idée de l’enchainement des tourbillons. Il imagina toute une cascade d’énergies, descendant vers des échelles de plus en plus réduites pour finalement atteindre une limite : les tourbillons sont alors si minuscules qu’ils sont absorbés par l’action comparativement importante de la viscosité.
Tout gaz ou liquide se compose de molécules individuelles si nombreuses qu’on peut les considérer en nombre infini. Si elles avaient chacune un mouvement indépendant, le fluide possèderait une infinité de comportements possibles
- un nombre de « degrés de liberté » infini dans le jargon des scientifiques
- et les équations décrivant le mouvement du fluide contiendraient une infinité de variables.
En réalité, le mouvement d’une molécule est fortement lié à celui de ses voisines, ce qui, dans un écoulement régulier, réduit considérablement le nombre de degrés de liberté. Il y a couplage de mouvements potentiellement complexes.
Des éléments de fluide voisins demeurent voisins au cours du mouvement,
ou s’éloignent lentement, linéairement, pour former, par exemple, les trainées bien dessinées que l’on observe sur les photos prises en soufflerie. Les particules de fumée qui s’élèvent d’une cigarette suivent toutes un temps le même mouvement.
L’Attracteur Etrange et l’Espace des Phases
L’attracteur étrange vit dans l’espace des phases, l’une des inventions les plus fécondes de la science moderne. L’espace des phases permet de transformer des nombres en images, de dégager l’essentiel de l’information d’un système – mécanique ou fluide – en mouvement, et de dresser la carte routière de toutes ses possibilités. Les physiciens connaissaient déjà deux types d’«attracteurs » élémentaires, les points fixes et les cycles limites, qui représentaient un mouvement atteignant un état stationnaire ou se reproduisant continuellement.
Dans l’espace des phases, la connaissance complète d’un système dynamique à un instant donné se réduit à un point. Ce point est le système dynamique – à cet instant. A l’instant suivant, le système évoluant, ne serait-ce que légèrement, ce point se déplace. On peut alors représenter l’histoire du système par ce point en mouvement, décrivant au cours du temps une « orbite » dans l’espace des phases.
Comment un seul point peut-il contenir toute l’information sur un système compliqué ? Si ce système ne possède que deux variables, la réponse est simple. Elle découle immédiatement de la géométrie cartésienne enseignée au lycée – on porte une variable sur l’axe horizontal, l’autre sur l’axe vertical. Si le système correspond au balancement sans frottement d’un pendule, ces deux variables sont la position et la vitesse ; leur variation continue dessine une boucle fermée que le point représentatif parcourt indéfiniment. Si le système possède une énergie plus élevée – un balancement plus rapide et plus ample -, on obtient une boucle analogue à la première, mais plus grande.
L’introduction d’un peu de réalisme – du frottement – modifie la figure. Les équations de mouvements ne sont pas indispensables pour connaître le destin d’un pendule soumis au frottement : toute orbite se doit d’aboutir au même endroit, l’origine des axes : position zéro, vitesse zéro. Ce point fixe central « attire » les orbites, qui, au lieu de décrire éternellement des boucles fermées, convergent suivant des spirales. La dissipation d’énergie due au frottement se traduit par une attraction vers le centre de l’espace des phases, des régions externes à haute énergie vers les régions internes d’énergie plus faible. Cet attracteur – le plus simple de tous – agit comme une tête d’épingle aimantée enfoncée dans une feuille élastique.
David Ruelle
David Ruelle soupçonna que les formes que l’on observait dans un écoulement turbulent – des lignes de courant entrelacées, des vortex, des tourbillons qui s’enflaient puis s’évanouissaient – étaient l’expression d’autres formes qui trouveraient leur explication dans des lois encore inconnues.
Dans son esprit, la dissipation d’énergie dans un écoulement turbulent devrait entrainer une contraction de l’espace des phases, une convergence vers un attracteur. Cet attracteur n’était certainement pas un point fixe : le fluide n’atteignait jamais le repos. L’énergie entrait dans le système tout autant qu’elle en sortait. De quel autre attracteur pouvait-il s’agir ? Selon la tradition, il n’existait qu’un seul autre type d’attracteur, un attracteur périodique, un « cycle limite », une orbite qui attirait toutes les orbites de son voisinage. Si un pendule reçoit son énergie d’un ressort et la perd par frottement – c’est à dire s’il est à la fois entretenu et amorti -, l’une de ses orbites stables dans l’espace des phases peut avoir la forme d’une boucle fermée, représentant par exemple l’oscillation régulière d’une pendule de grand-mère.
Ruelle et Takens
Ruelle et Takens se demandèrent s’il n’existait pas un autre attracteur possédant les bonnes propriétés : stable – représentant l’état final d’un système dynamique dans un univers de bruit -, de faible dimension – une orbite dans un espace des phases à deux ou trois dimensions, avec seulement quelques degrés de liberté – non périodique – ne se répétant jamais, ni n’atteignant la périodicité régulière d’une horloge de grand-mère.
Au niveau géométrique, ce problème constituait une énigme : quel type d’orbite pouvait-on dessiner dans un espace limité qui ne se reproduirait jamais ni ne se recouperait jamais – car une fois qu’un système retrouve un état qu’il a déjà occupé, il doit alors reprendre la trajectoire qui l’y a amené. Pour reproduire toutes les fréquences, cette orbite devait avoir une longueur infinie contenue dans une surface finie. En d’autres termes, elle devait être fractale.
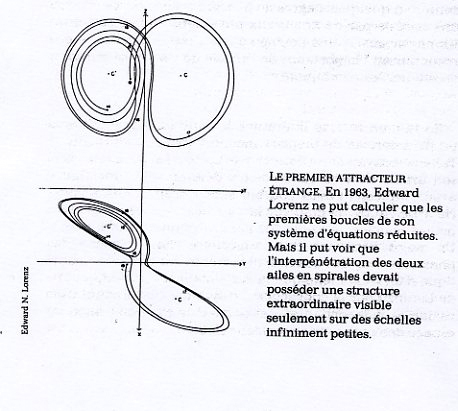
Attracteur de Lorenz
Cet attracteur était stable, de faible dimension, et non périodique. Il ne pouvait se recouper – jamais – et c’est ce qui faisait sa beauté. Ces boucles et ces spirales se serraient à l’infini, sans jamais réellement se joindre, sans jamais s’intersecter. Pourtant elles demeuraient à l’intérieur d’un espace fini, dans un cube. Comment était-ce possible ? Comment une infinité de trajectoires pouvait-elle exister dans un espace fini ?

Otto Rössler
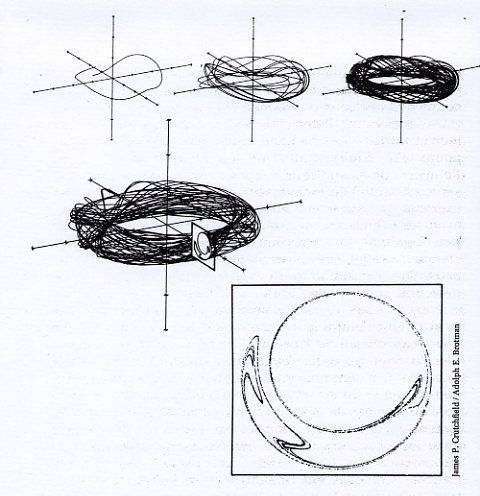
Otto Rössler, un médecin non praticien, venu au chaos par la chimie et la biologie théorique, développa une aptitude singulière à considérer les attracteurs étranges comme des objets philosophiques, reléguant à l’arrière-plan leur aspect mathématique. Son nom resta attaché à un attracteur particulièrement simple, un ruban contenant un pli ; il envisagea également des attracteurs de dimensions plus grandes – « une saucisse dans une saucisse dans une saucisse dans une saucisse, disait-il, prenez-la, pliez-la, contractez-la, et reposez-là ». Les pliages et les contractions de l’espace étaient justement la clé permettant de construire des attracteurs étranges, et peut-être aussi la clé de la dynamique des systèmes réels qui leur donnait naissance. Rössler avait le sentiment que ces formes recelaient un principe auto-organisateur de l’univers.
Attracteur de Hénon
L’attracteur qui apporta le plus d’éclaircissements, parce qu’il était le plus simple, est dû à un homme très éloigné des mystères de la turbulence et de la mécanique des fluides. Cet homme, Michel Hénon, était astronome à l’observatoire de Nice. En un sens, c’est bien sûr l’astronomie qui a donné naissance aux systèmes dynamiques : le mouvement régulier des planètes fit le succès de Newton, et Laplace y puisa son inspiration. Mais la mécanique céleste diffère de la plupart des systèmes terrestres sur un point essentiel. Les systèmes qui perdent leur énergie par frottement sont dissipatifs. Ce n’est pas le cas des systèmes astronomiques : ils sont conservatifs – ou hamiltoniens. En réalité, sur une échelle pratiquement infinitésimale, les systèmes astronomiques subissent eux aussi une forme de frottement : les étoiles rayonnent de l’énergie et la friction des marées freine les corps sur leurs orbites.
Mais bien avant cette époque, il s’était lancé sur un problème de dynamique particulièrement déroutant : celui des amas globulaires – des groupements sphériques pouvant contenir jusqu’à un million d’étoiles, les plus anciens et certainement les plus stupéfiants des objets du ciel nocturne. Ces amas possèdent une densité d’étoiles fantastique. Leur stabilité et leur évolution avaient intrigué les astronomes au cours du XXe siècle.
Conception de l’attracteur de Hénon
Sur une échelle de temps de quelques deux cents millions d’années, les orbites stellaires au sein d’une galaxie ne plus des ellipses parfaites : elles ont des caractéristiques tridimensionnelles. Ces orbites tridimensionnelles sont aussi difficiles à visualiser dans la réalité que lorsqu’elles sont des constructions fictives dans l’espace des phases. Hénon utilisa alors une technique comparable à l’application du premier retour de Poincaré. Il imagina une feuille de papier disposée perpendiculairement d’un côté de la galaxie de manière à être traversée par toutes les orbites, comme des chevaux sur un champ de courses franchissant la ligne d’arrivée. Puis il marqua le point où une orbite intersectait ce plan et en suivit le mouvement pour chaque révolution.
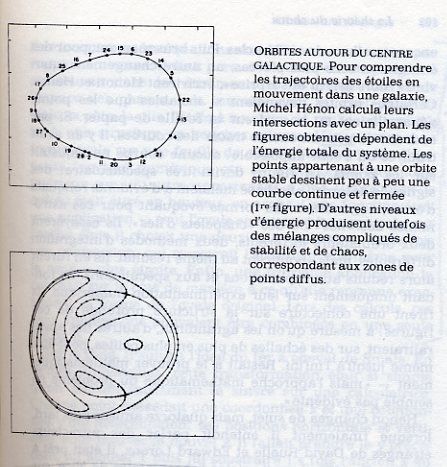
Les nombreux scientifiques qui, plus tard, recoururent à cette technique, n’eurent qu’à observer l’apparition de ces points sur un écran d’ordinateur, comme des réverbères s’allumant l’un après l’autre au crépuscule. Hénon, lui, devait les tracer à la main. Une orbite typique pouvait débuter par un point en bas à gauche de la feuille. Au tour suivant, un autre apparaissait, quelques centimètres vers la droite, puis un troisième, un peu plus vers la droite et légèrement plus haut – et ainsi de suite. Au début, on ne distinguait aucun motif évident ; mais après une dizaine ou une vingtaine de points, une courbe ovoïde commençait d’émerger. En fait, les points successifs décrivaient une ronde sur la courbe sans repasser exactement au même endroit, et au bout de centaines ou de milliers de ces points, la courbe était parfaitement dessinée.
Hénon décida une nouvelle fois d’écarter toute référence aux origines physiques du système pour se concentrer sur son aspect géométrique. Alors que Lorenz et les autres chercheurs restaient fidèles aux équations différentielles – des flots, avec des variations continues dans l’espace et le temps -, il se tourna vers les équations aux différences, discrètes par rapport au temps. Il était persuadé que la clé du problème se trouvait dans les étirements et les pliages itérés de l’espace des phases, à la manière dont un chef pâtissier étale sa pâte, la plie, l’étale à nouveau, la replie, pour aboutir à une structure en couches minces. Hénon traça une forme ovale sur une feuille de papier, l’étira à l’aide d’une petite fonction numérique qui en transportait tout point intérieur sur un autre appartenant à une figure dont le milieu était étiré en hauteur, en arche. Cette fonction était une application – tout l’ovale se retrouvait « appliqué » sur l’arche. Puis il choisit une deuxième application, cette fois une contraction, qui resserrait l’arche sur elle-même pour la rendre plus étroite. Enfin, une troisième application la couchait sur le côté de manière à ce qu’elle reprenne exactement la forme de l’ovale original. Lors des calculs, ces trois applications pouvaient être combinées en une seule fonction.
Les attracteurs étranges – Principes
Sur le plan théorique, l’attracteur étrange permettait d’exprimer mathématiquement les nouvelles propriétés fondamentales du chaos. La dépendance sensitive aux conditions initiales était l’une de ces propriétés. Le « mixing » en était un autre, qui prendrait toute sa significations, par exemple, dans la conception des moteurs à réaction pour obtenir un mélange efficace de carburant et d’oxygène. Mais personne ne savait comment mesurer ces propriétés, comment les exprimer par des nombres. Les attracteurs étranges paraissaient de nature fractale, ce qui signifiait que leur véritable dimension devait être fractionnaire, mais personne ne savait comment mesurer cette dimension ou comment appliquer sa mesure aux problèmes des ingénieurs.
Plus important, personne ne savait si les attracteurs étranges donneraient une indication sur le très profond problème des systèmes non linéaires. Contrairement aux systèmes linéaires, que l’on avait facilement résolus et classés, les systèmes non linéaires semblaient encore, fondamentalement, échapper à toute classification – chacun différait des autres. Les scientifiques commencèrent à soupçonner qu’ils avaient en commun certaines propriétés, mais lorsque vint le temps de faire des mesures et d’effectuer des calculs, chaque système non linéaire apparut comme un monde en soi. En comprendre un ne semblait d’aucune utilité pour comprendre le suivant. Si un attracteur comme celui de Lorenz illustrait la stabilité et la structure cachée d’un système qui autrement en semblait dépourvu, comment cette double spirale particulière pouvait-elle aider les chercheurs à explorer des systèmes sans relation entre eux ? Personne ne le savait.
Les argiles Vie Espace Temps® sont construites et informées par des attracteurs étranges permettant de transférer une énergie linéaire destructurante pour le Système Neurovégétatif et le Vivant en une énergie chaotique bien plus proche des fonctions vitales. On transcende ainsi la quatrième dimension
Toutes les fonctions vitales sont soumises à des attracteurs étranges, véritables potentiels organisateurs du Vivant. Les champs électromagnétiques, téléphones portables, Wifi, sont des énergies linéaires destructurantes en augmentant l’entropie.



